Medidas de Tendencia Central (datos no agrupados)
Se les llama medidas de tendencia central a la media aritmética, la mediana, la media geométrica, la moda, etc. debido a que al observar la distribución de los datos, estas tienden a estar localizadas generalmente en su parte central.
En matemáticas y estadística, la media aritmética (también llamada promedio o simplemente media) de un conjunto finito de números es igual a la suma de todos sus valores dividida entre el número de sumandos.
Expresada de forma más intuitiva, podemos decir que la media aritmética: Es la suma de todos los valores dividida por el número de datos. Solo es aplicable para el tratamiento de datos cuantitativos.
La media aritmética destaca por representar el reparto equitativo, el equilibrio, la equidad, ya que es el valor que tendrían los datos, si todos ellos fueran iguales. O, también, el valor que correspondería a cada uno de los datos de la distribución si su suma total se repartiera por igual.
La media aritmética está dada por la fórmula:
Ejemplo:
Se tienen las edades de cinco estudiantes universitarios de 1er año, a saber: 28,23, 27,34 y 25., para calcular la media aritmética del promedio de las edades, se tiene que:
Una media cuadrática se define como la raíz cuadrada de la media aritmética de los cuadrados de los valores de la variable.
Para datos no agrupados su formula puede expresarse como:
Ejemplo:
2, 5, 7, 8, 3, 2, 4, 6, 7, 7,
Paso 1: Elevar cada dato al cuadrado: 4, 25, 49, 64, 9, 4, 16, 36, 49, 49
Pasó 2: Sumar los datos elevados al cuadrado: 4+25+49+64+9+4+16+36+49+49 = 305
Pasó 3: aplicar la fórmula
La media cuadrática es 5.52
En matemáticas y estadística, la media geométrica de una cantidad arbitraria de números (digamos n números) es la raíz n-ésima del producto de todos los números.
Ventajas y Desventajas:
· En su cálculo intervienen todo los valores de la distribución.
· Los valores extremos tienen menor influencia que en la media aritmética.
· Es única
· Su cálculo es más complicado que el de la media aritmética.
· Solo se puede calcular si no hay observación negativa.
La formula para su cálculo es:
Donde MG es media geométrica, “n” es el número total de datos y “x” es el valor de cada observación de la variable de interés.
Ejemplo:
Las siguientes temperaturas han sido tomadas de un proceso químico 7, 5 y 4 determine la temperatura promedio de este proceso.
La media armónica, denominada H, se define como la reciproca de la media aritmética de los recíprocos de un conjunto de datos.
La media armónica resulta poco influida por la existencia de determinados valores mucho más grandes que el conjunto de los otros, siendo en cambio sensible a valores mucho más pequeños que el conjunto.
Ventajas y Desventajas:
· En su cálculo intervienen todos los valores de la distribución.
· Su calculo no tiene sentido cuando algún valor de la variable tomo valor cero.
· Es única.
La formula correspondiente para su cálculo es la siguiente:
Donde H es la media armónica, “n” es el numero de datos, “x” cada valor observado correspondiente a la variable de interés.
Ejemplo:
Determine la media armónica de los siguientes datos, 3, 2, 6:
Mediana (Me):
En el ámbito de la estadística, una mediana es el valor de la variable que deja el mismo número de datos antes y después que él, una vez ordenados estos. De acuerdo con esta definición el conjunto de datos menores o iguales que la mediana representarán el 50% de los datos, y los que sean mayores que la mediana representarán el otro 50% del total de datos de la muestra.
La mediana toma en cuenta la posición de los datos y se define como el valor central de una serie de datos.
El primer paso es ordenan los datos y luego se determina el valor central de la serie (la posicion) y esa es la mediana. Si el número de datos es par, existirán dos valores centrales y entonces la mediana se obtiene sacando el promedio de ellos.
Existen dos estrategias para calcular la mediana:
a) Si “n” es impar la formula es:
Los siguientes datos son las mediciones obtenidas de un circuito utilizado en un arnés de lavadora; se toman como muestra cinco circuitos y sus mediciones son: 3, 6, 7, 8, 9 encontrar la mediana:
b) Si “n” es par la formula es:
Ejemplo:
De los siguientes números cuál es el que está en el centro.
12, 15, 17, 19, 20, 23, 25, 27, 30, 36
Si el número de casos es par hay dos datos, por lo tanto deberá calcularse la media aritmética de ambos casos. Para el caso de la pantalla anterior
(20+23) ÷ 2 = 21.5
La mediana es 21.5
La moda es el valor que aparece con mayor frecuencia en la serie de datos. La moda es una medida muy natural para describir un conjunto de datos; su concepto se adquiere fácilmente: es la altura más corriente, es la velocidad más común, etc. Además tiene la ventaja de que no se ve afectada por la presencia de valores altos o bajos.
La principal limitación esta en el hecho de que requiere un número suficiente de observaciones para que se manifieste o se defina claramente.
Otros inconvenientes son que puede darse el caso de que una determinada serie no tenga moda o que tenga varias modas.
Ventajas y Desventajas:
· La moda tiene la ventaja de no ser afectada por valores extremos.
· Al igual que la mediana, puede ser calculada en distribuciones con intervalos abiertos.
· En algunas series de datos hay más de una moda, en este caso uno podría preguntarse ¿cual es el valor representativo de la serie de datos?
· En muchas series de datos no hay moda porque ningún valor aparece más de una vez.
Ejemplo:
Determine la moda de los datos que se muestran a continuación, se refieren a la estatura de un grupo de jóvenes {14, 15, 17, 17, 21, 21, 21, 33, 36, 40}:
El dato que más se repite es 21 por lo tanto esa es la moda.
Trabajo realizado por:
Malitzin Tayasal Marlene Saloj Oroxom










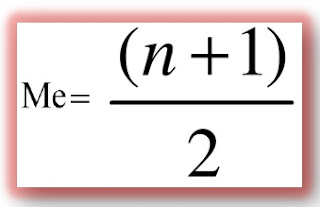



No hay comentarios:
Publicar un comentario